一个奇怪的做法

题目链接：P5179 【Fraction】

反正也有一个 $log$ 的题解了，我就来搞一个比较好玩的两个 $log$ 做法。

题目要我们求满足 $\dfrac{a}{b} < \dfrac{p}{q} < \dfrac{c}{d}$ 的最简分数 $\dfrac{p}{q}$，并满足 $q$ 最小，然后满足 $p$ 最小。

可以放在平面直角坐标系里面，把 $(q,p)$ 当做一个点表示出来。发现若两侧取等，则 $(q,p)$ 分别过直线 $p=\dfrac{a}{b}q$ 和 $p=\dfrac{c}{d}q$，其中 $q$ 是自变量。

比如样例中的 a=1,b=3,c=1,d=2，可以表示为：

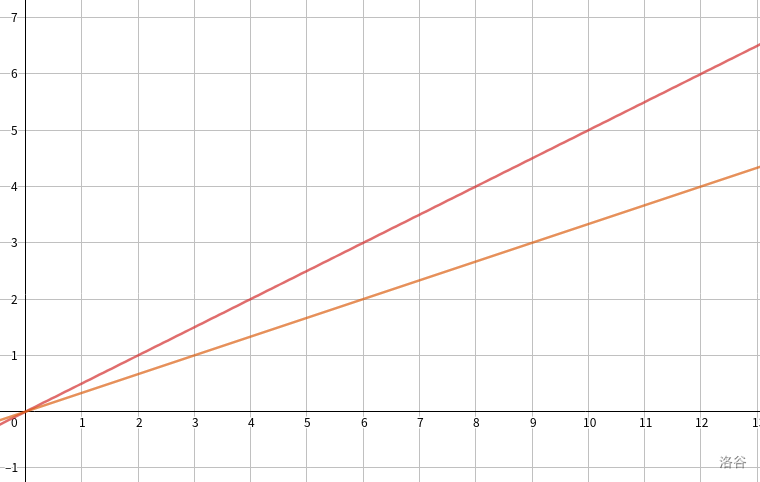
那么点 $(q,p)$ 一定严格在两条直线中间，并显然这个点是一个整点 废话。

那么现在我们希望得到的是满足条件的整点中最左边的那一个，因为他能满足 $q$ 最小的条件。能够发现这个点 $(q,p)$ 一定满足 $gcd(p,q)=1$，因为如果 $gcd(p,q) \ne 1$，那么一定有 $(\dfrac{q}{gcd(p,q)},\dfrac{p}{gcd(p,q)})$ 也满足条件，并且他在更左边。

如果把直线 $x=q$ 加入图像，并计算这三条直线围成图形中的整点个数（直线 $x=q$ 上的整点算入总数，其他两条直线上的整点不算）。

当 a=1,b=3,c=1,d=2,q=5 时，重合的部分如下：

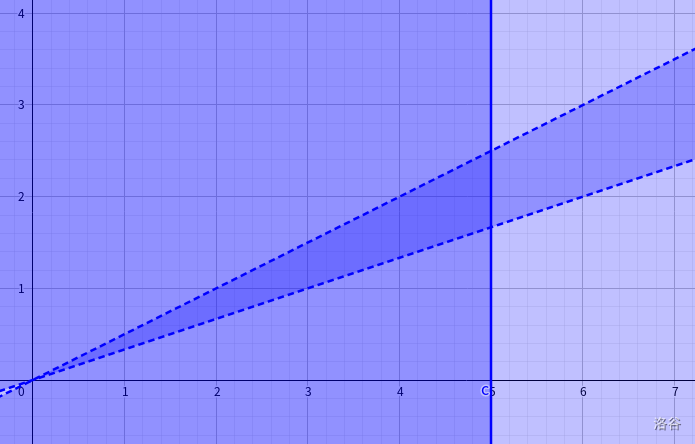
好丑的图

不难发现两个直线中间的整点个数随着 $q$ 的增大而单调不减，所以我们可以二分 $q$，找出最小的 $q$ 满足范围内的整点个数 $\ge 1$ 即可。

如何求这个区间内的整点个数呢？

可以考虑差分，分别计算两个正比例函数下方的整点个数，再相减。

现在的问题转化为：求正比例函数 $y=\dfrac{a}{b}x$ 下方的整点个数。其实就是：

$$\sum_{i=0}^{q} \lfloor \dfrac{a\times i}{b} \rfloor$$

这就是个类欧几里得的板子。

那么我们对两个正比例函数分别做一次类欧，然后进行差分，如果整点个数 $\ge 1$，说明这个 $q$ 满足条件，二分右端点左移，否则二分左端点右移。

需要注意的是，类欧几里得的板子会计算到直线上的整点，我们需要减去他们，但只需要减去在上方的直线上的整点个数即可，因为下方直线上的点也需要被减去，所以不需要特殊考虑。

现在我们就可以找到最小的 $q$ 了，最小的 $p$ 是多少呢？若令 $\dfrac{a}{b} > \dfrac{c}{d}$，那么显然 $p=\lfloor \dfrac{c \times q}{d} \rfloor + 1$。

因此复杂度为 $O(T\log^2\text{值域})$ 的样子吧。

注意二分上界的问题，要尽量开大，同时需要考虑爆 $\texttt{long long}$ 的情况，懒人 $\texttt{CXY07}$ 用了 __$\texttt{int128}$。

//Code By CXY07
#include<bits/stdc++.h>
using namespace std;

//#define FILE
#define int __int128
#define LL long long
#define pii pair<int,int>
#define mp make_pair
#define pb push_back
#define fst first
#define scd second
#define inv(x) ksm(x,mod - 2)
#define lowbit(x) (x & (-x))

const int MAXN = 1;
const int INF = 4e9;
const double PI = acos(-1);
//const int mod = 1e9 + 7;
//const int mod = 998244353;
//const int G = 3;

LL a,b,c,d;

template<typename T> inline void read(T &a) {
    a = 0; char c = getchar(); int f = 1;
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') {a = a * 10 + (c ^ 48); c = getchar();}
    a *= f;
}

void out(int x) {
    if(!x) return;
    out(x / 10);
    putchar(x % 10 + '0');
}

int gcd(int x,int y) {
    if(!y) return x;
    return gcd(y,x % y);
}

int calc(int n,int a,int b,int c) {
    if(!a) return (n + 1) * (b / c);
    if(a >= c || b >= c) return (n + 1) * n / 2 * (a / c) + (n + 1) * (b / c) + calc(n,a % c,b % c,c);
    int m = (a * n + b) / c;
    return n * m - calc(m - 1,c,c - b - 1,a);
}

bool chk(int x) {
    int res = calc(x,a,0,b) - calc(x,c,0,d);
    res -= x / b;//减去上方直线上的整点
    return (res >= 1);
}

void solve() {
    int L = 1,R = INF,mid;//注意R的上界
    while(L < R) {
        mid = (L + R) >> 1;
        if(chk(mid)) R = mid;
        else L = mid + 1;
    }
    out(c * L / d + 1); putchar('/'); out(L);
    putchar('\n');
}

signed main () {
#ifdef FILE
    freopen(".in","r",stdin);
    freopen(".out","w",stdout);
#endif
    while(~scanf("%lld%lld%lld%lld",&a,&b,&c,&d)) {
        //read(a); read(b); read(c); read(d);
        int ab = gcd(a,b),cd = gcd(c,d);
        a /= ab,b /= ab,c /= cd,d /= cd;//把分数化简
        if(a * d < b * c) swap(a,c),swap(b,d);//强行让 (a / b) > (c / d)
        solve();
    }
    return 0;//sto zxyhymzg orz
}