IOI2020国家集训队作业试题乱做 Part 4

难度标签：$\color{red}\texttt{[HARD]}$，$\color{blue}\texttt{[NORMAL]}$，$\color{green}\texttt{[EASY]}$。

CF575I Robots protection

$\color{blue}\texttt{[NORMAL]}$

发现一个等腰直角三角形可以通过对三个量的限制进行维护，分别是 $x,y,x+y$。加上时间就是四维偏序问题，复杂度是 $\mathcal{O}(q\log^3 q)$，无法通过。

考虑从等腰直角三角形的一些性质出手，现在只讨论直角在左下方的情形。发现若边长是 $l$，那么首先需要满足 $(x'+y')\in [x+y, x+y+l]$，这些点的分布长这样：

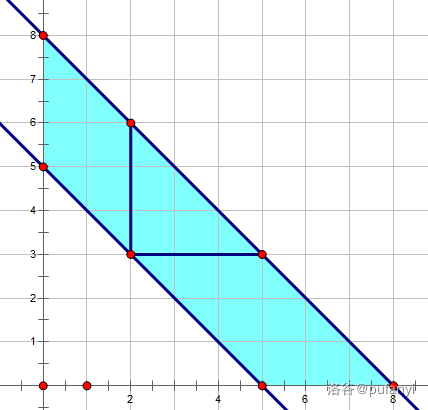
那么需要减去：

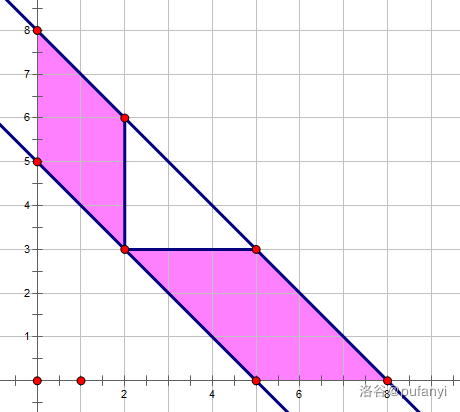
发现减去的部分不过就是在 $x$ 或者 $y$ 上多了一个限制，所以就可以认为少了一个维度，二维树状数组即可。

时间复杂度 $\mathcal{O}(q\log^2 n)$，空间复杂度 $\mathcal{O}(n^2+q)$。

CF582E Boolean Function

$\color{blue}\texttt{[NORMAL]}$

发现给出的取值点很少($16$)，考虑如何利用。

首先建立表达式树，然后考虑在上面进行 $\text{dp}$。结合之前所得到的取值点少的性质，我们不难得到这样一个状态：

设 $\text{dp}_{x,S}$ 表示，$x$ 这个点的子树内，每一种给出的取值方案的值状压起来是 $S$ 的方案数。

显然可以直接 $\text{FWT}$ 优化一下转移，复杂度 $\mathcal{O}(|S|n2^n)$。

CF611H New Year and Forgotten Tree

$\color{red}\texttt{[HARD]}$

$\text{Hall}$ 定理：

若二分图 $(X,Y)$ 存在完美匹配，则令 $|X|\le|Y|$，对于任意 $S\subseteq X$，$S$ 连接的 $Y$ 部点个数均需 $\ge |S|$。

发现相同位数的数字是没有区别的，因此只看位数，称之为颜色。钦定 $1$ 号点为根，那么剩下的部分可以看做是 边 与 边指向的深度较深的点 的匹配，若存在完美匹配则有解，判断可以用 $\text{Hall}$ 定理做到单次 $\mathcal{O}(2^m\times m^2)$，其中 $m=\lfloor\log_{10} n\rfloor$，暴力枚举子集即可。

每次暴力枚举，选择两个颜色，看是否能在这两种颜色的点之间连一条边，然后再判断是否仍然存在完美匹配，若存在则可行。

CF611G New Year and Cake

$\color{blue}\texttt{[NORMAL]}$

设 $\text{area}(a, b)$ 表示点 $p_a,p_{a+1}\cdots p_{b-1}, p_{b}$ 这些点组成的多边形的面积，$S=\text{area}(1,n)$。

对于一种划分方案的面积 $A, B(A+B=S,A\le B)$，$|A-B|=S-2A$，因此只需要找出所有的较小的一部分即可。

考虑对于每一个点 $x$，找到一个点 $y$ 使得 $y$ 是顺时针最后一个点使得 $\text{area}(x,y)\le \left\lfloor\dfrac{S}{2}\right\rfloor$。易于发现在 $x,y$ 之间的所有三角形的出现次数就是一个公差为 $-1$ 的等差数列，这个可以通过维护前缀和来求得。

不只是这个等差数列，还有 $\sum_{i=x}^y |p_x\times p_i|$，由于 $i$ 在 $x$ 的同一侧，所以这等价于 $p_x\times (\sum_{i=x}^y p_i)$，可以通过维护 $p_i$ 的前缀和来求解。

至于维护 $x,y$，显然可以双指针。复杂度 $\mathcal{O}(n)$，可能需要 $\text{unsigned long long}$，需要注意溢出的问题。

CF575E Spectator Riots

$\color{green}\texttt{[EASY]}$

意思实际上就是有若干区域，每个区域内等概率随机出现一个点，现在要从区域的并中取出三个点作外接圆，期望能够盖住尽量多的出现的点，在这个基础上最大化圆的半径。

发现根本不需要管随机出现这回事，因为只要把所有区域全部盖住就好了。那么把所有边界点都拿出来求个凸包，答案必然是凸包上某三个点的外接圆。考虑如何使半径最大，直线是半径最大的，但是不能取直线，所以答案一定是凸包上连续三个点。

设三角形三边长 $a,b,c$，面积为 $S$，那么外接圆半径是：

$$ \dfrac{abc}{4S} $$

时间复杂度 $\mathcal{O}(n\log n)$。

CF626G Raffles

$\color{blue}\texttt{[NORMAL]}$

设 $E(x)$ 是某一堆放 $x$ 张的期望得分，那么 $E(x)=\dfrac{p_i\times x}{l_i+x}$，若多放一张，则 $\Delta E(x)=p_i(\dfrac{x+1}{l_i+x+1}-\dfrac{x}{l_i+x})=p_1\dfrac{l_i}{(x+l_i)(x+l_i+1)}$，显然 $\Delta E(x)$ 是减函数。那么可以用堆维护，每次选择最大的 $\Delta$，在那里 $x+1$。

考虑修改，此处只考虑 $+1$，$-1$ 类似。有结论：

修改之后，至多有一张彩票的位置发生改变。

在修改前：

$$ \Delta E(x)=p_i\dfrac{l_i}{(x+l_i)(x+l_i+1)} $$

$$ \Delta E(x+1)=p_i\dfrac{l_i}{(x+l_i+1)(x+l_i+2)} $$

修改后：

$$ \Delta E'(x)=p_i\dfrac{l_i+1}{(x+l_i+1)(x+l_i+2)} $$

$$ \Delta E'(x+1)=p_i\dfrac{l_i+1}{(x+l_i+2)(x+l_i+3)} $$

容易知道：$\Delta E(x)>\Delta E(x+1),\Delta E'(x)>\Delta E'(x+1)$ 且可以发现 $\Delta E'(x)>\Delta E(x+1)$。若修改前最小贡献是 $\Delta E_{\min}$，修改后是 $\Delta E'_{\min}$，那么 $\Delta E_{\min}>\Delta E'_{\min}$。

若 $x,x+1$ 原本都是被选择的，修改后都不被选择，那么：

$$ \Delta E(x+1)>\Delta E_{\min} $$

$$ \Delta E'(x)<\Delta E'_{\min} $$

可以推出 $\Delta E'(x)<\Delta E'_{\min}<\Delta E_{\min}<\Delta E(x+1)$，这与 $\Delta E'(x)>\Delta E(x+1)$ 不符，所以不可能 $x,x+1$ 都变得不优。于是拿 $\text{multiset}$ 维护即可。

复杂度 $\mathcal{O}((n+t+q)\log n)$。

CF613E Puzzle Lover

$\color{blue}\texttt{[NORMAL]}$

发现只有两行，所以路径的形式实际上是很局限的。画一画发现，一条路径一定长成：两侧是两个类似 $\texttt{U}$ 字形，中间是“上下上下”摆动。不难发现中间部分只能朝一个方向移动。

设是往右走，往左边直接 $\text{reverse}$ 再做一遍即可。

考虑根据这个来 $\text{dp}$。设 $\text{dp}_{x,y,k,0/1}$ 表示当前在位置 $(x,y)$，已经匹配到 $k$，上面/下面那个点是否已经走过的方案数。然后枚举当前这一步是向右边走还是向上/下走，这就可以得到中间部分的转移。至于两侧，容易通过 $\text{hash}$ 来得到所有可行的 $\texttt{U}$，和中间的 $\text{dp}$ 接起来即可。

时间复杂度 $\mathcal{O}(n^2)$。

CF607E Cross Sum

$\color{red}\texttt{[HARD]}$

把询问点作为坐标原点，然后二分一个半径。考虑计算这个圆中的交点个数，发现如果一条直线将圆划成两条弧，另一条直线两个端点分别落在两条弧上，那么这两条直线有交。可以把交点都求出来，极角排序之后变成区间问题：

给定若干区间，问有多少区间 $[l_1,r_1],[l_2,r_2]$ 满足 $l_1\le l_2\le r_1\le r_2$。

这个可以树状数组来维护。然后二分出一个半径 $r$，考虑所有距离 $<r$ 的交点（注意是小于，不能取等），总数一定 $<m$，因此考虑求出每一个距离 $<r$ 的交点，然后求距离，剩下的点都认为是在圆周上。

至于计算距离 $<r$ 的交点的距离，可以做上面二分的时候差不多的东西，唯一不同的是把树状数组换成 $\text{set}$ 维护区间信息，每次暴力查找和一个区间交叉的区间，然后求直线交点即可。

时间复杂度 $\mathcal{O}(n\log n\log w+m\log n)$。这题评到这个分极大程度由于代码精度的精神污染

CF587F Duff is Mad

$\color{red}\texttt{[HARD]}$

令 $m=\sum |s_i|$。

一个比较自然的想法是对区间分块，但是不好处理单点对单点的贡献。发现 $m\le 10^5$，因此考虑根号分治。同时，需要注意这个东西具有可减性，也就是在一定情况下，是可以做差分的。

设一个分治的阈值 $T$。对于 $|s_i|>T$ 的情况，这样的串至多 $\dfrac{m}{T}$ 个，考虑单次 $\mathcal{O}(n)$ 地计算所有可能的贡献。那么转化为计算每一个前缀的答案，再转化为计算一个字符串的答案再做前缀和。建立 $\text{AC}$ 自动机，发现可以取出这个串 $s$ 的每一个前缀对应的点，把这个点的权值 $+1$，那么对于另一个串 $t$，其在 $s$ 中的出现次数就是 $t$ 在 $\text{trie}$ 树上的终止节点，在 $\text{fail}$ 树上对应节点的子树内的权值和。

事实上就是枚举这个串 $t$ 在 $s$ 中的结尾位置，然后通过跳 $\text{fail}$ 来在 $t$ 的前面加字符。这样，就可以算出单个串的答案的前缀和，从而求解这个串的所有答案，单次复杂度 $\mathcal{O}(m)$。

再考虑 $s_i\le T$ 的情形。考虑设计一个单次 $\mathcal{O}(|s_i|)$ 的做法。同样利用差分的想法，将区间询问拆成两个前缀询问。

刚刚是先枚举了 $s_i$ 的每一个节点做预处理，然后再枚举每一个串。这里由于 $|s_i|$ 不大，所以可以先枚举出一个串做预处理，然后再在 $\text{trie}$ 上取出 $s_i$ 的每一个节点来求一些答案。

之前是枚举结尾位置，这里类似。在 $\text{trie}$ 上取出 $s_i$ 的每一个节点的时候，我们考虑求出以当前点作为结尾的答案个数。实际上就是当前前缀去掉一个前缀后得到的串个数，这就是该点的 $\text{fail}$ 链上的结尾标记个数。

考虑离线，加入一个新串的时候，取出其结尾位置，在 $\text{fail}$ 树的子树内 $+1$，查询的时候查询单点即可。时间复杂度是 $\mathcal{O}(qT\log m)$。

所以复杂度是 $\mathcal{O}(\dfrac{m^2}{T}+qT\log m)$，在 $T=\dfrac{m}{\sqrt{q\log m}}$ 的时候达到最优复杂度 $\mathcal{O}(m\sqrt{q\log m})$。

CF704E Iron Man

$\color{red}\texttt{[HARD]}$

首先考虑链怎么做。考虑二分答案，把每个人都移动一下，然后进行排序。如果排序前后的顺序不同了，说明有人相撞导致了交换。这样是 $\mathcal{O}(n\log^2 n)$ 的。

事实上可以做到 $\mathcal{O}(n\log n)$。把一个点 $a$ 时刻在 $x$ 点描述为一个二维点 $(a,x)$，那么一次移动就是一条二维平面上的线段。画画图发现，若两个人会相撞，当且仅当两条线段相交了。那么要找横坐标最小的交点，就代表着最早的相撞时间。

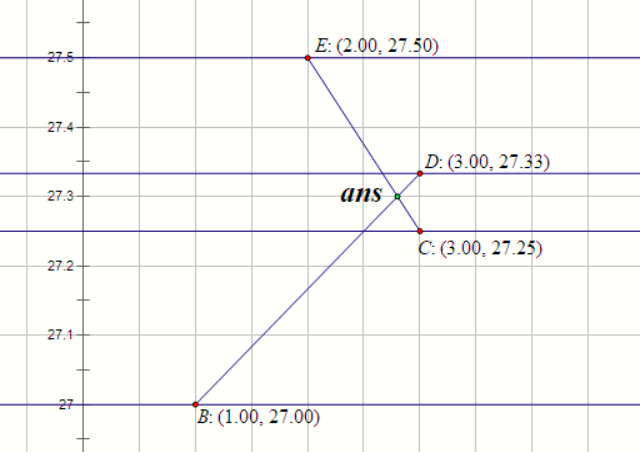
考虑扫描线，从左往右按照时间扫描。可以发现若两条线段可能成为最优解，当且仅当在某一个 $x$ 上，两条线段的 $y$ 是相邻的（反证），因此可以直接拿 $\text{set}$ 维护当前 $x$ 的所有 $y$，每次需要插入/删除一个点，求相邻两条线段的交点。需要注意的是，在线段相交之后，$\text{set}$ 中原本的顺序关系就会发生变化，但是事实上我们只需要找第一个相交的位置。所以在动态更新答案的同时，若当前的 $x$ 已经大于我已经得到的最优解，则直接结束，这样即可保证顺序不变。

那么这样就可以做到 $\mathcal{O}(n\log n)$。

考虑放到树上怎么做。自然的想法是将路径拆掉，但是怎么拆是一个问题。考虑将树重链剖分，一条路径就被划分为 $\mathcal{O}(\log n)$ 段，每一段上做序列的问题，答案取 $\min$ 即可。

由于拆了路径，所以时间复杂度是 $\mathcal{O}(m\log n\log m)$。