【学习笔记】格路计数相关

前言

不知道是不是群除我会

本学习笔记基本参考【IOI2019 论文集】戴言，浅谈格路计数相关问题

大概会把一车定义直接贴过来

以下没有申明处均认为 $\gcd(n,m)=1$。

$\text{Dyck}$ 路

格路

在平面直角坐标系中，横坐标和纵坐标都是整数的点称为 格点，平面格路 是指从一个格点到另一格点只走格点的路，格路的 长度 是指其所走的路的步数。

自由路

对于一条从 $(0, 0)$ 到 $(n, m)$ 的格路，若其只使用了上步 $U = (0, 1)$，水平步 $L = (1, 0)$ ，则我们称其为 $(n, m)$ 自由路。

设 $\mathcal{F}(n,m)$ 是 $(n,m)$ 自由路的集合，$F(n,m)$ 表示从 $(0,0)$ 到 $(n,m)$ 的自由路条数，则显然：

$$ F(n,m)=\binom{n+m}{n} $$

$(n,m)-\text{Dyck}$ 路

对于一条从 $(0, 0)$ 到 $(n, m)$ 的自由路，若其始终不经过对角线 $y = \dfrac{m}{n}x$ 下方，则我们称之为 $(n, m)-\text{Dyck}$ 路。

设 $\mathcal{D}(n,m)$ 是 $(n,m)-\text{Dyck}$ 路的集合，$D(n,m)$ 是条数。

对于从 $(0, 0)$ 到 $(n, m)$ 的 $2$ 条格路 $P, Q$，其中 $P = u_1 u_2\cdots u_{n+m},Q = v_1 v_2\cdots v_{n+m},(u_i,v_i \in \{L, U\}, i \in [1,n+m])$。
若 $\exists i, u_{i+1}\cdots u_{n+m} u_1\cdots u_i = v_1 v_2\cdots v_{n+m}$，则我们称格路 $P, Q$ 等价。将 $P$ 的等价格路全集记为 $[P]$。

就意思是 $P,Q$ 循环同构，就称他们等价。

对于任意格路 $P$，记 $P_k = u_{k+1} u_{k+2}\cdots u_{n+m} u_1\cdots u_k$，则 $[P] = \{P_k | k \in [1,n+m]\}$。定义 $P$ 的周期为使得 $P = P_k$ 的最小数 $k$，用 $\text{period}(P)$ 表示，则显然有 $|[P]| = \text{period}(P)$。

大概可以类比字符串的 $\text{period}$。现在给出一个引理：

若 $\gcd(n,m)=1$，则 $\forall P\in\mathcal{F}(n,m)$，有：

$$ \text{period}(P)=n+m $$

可以使用反证法，但是我鸽了。接下来考虑这个 $\text{period}$ 和 $\text{Dyck}$ 路有啥关系。

若 $\gcd(n,m)=1$，则 $\forall P\in \mathcal{F}(n,m)$，$[P]$ 中有且仅有一条 $(n,m)-\text{Dyck}$ 路。

证明：

存在性：

对于 $P\in \mathcal{F}(n,m)$，若 $P$ 是一条 $(n,m)-\text{Dyck}$ 路，则直接存在了。否则一定有一点在 $y=\dfrac{m}{n}x$ 下方。设对角线下方距离 $y=\dfrac{m}{n}x$ 最远的点是 $s$，把 $P$ 按 $s$ 划分为两段 $P_1, P_2$，则 $P'=P_2 P_1$ 是一条 $\text{Dyck}$ 路。

感性理解的话，可以认为是 $P_2$ 的总体“斜率”比较大，放在前面更好，而且 $s$ 已经是距离对角线最远的了，所以成立。但是还只会感性理解为啥只有距离对角线最远的点可以做到这个事情，证明先鸽。

唯一性：

那唯一性说明的就是，在对角线下方，距离对角线最远的点唯一。反证，假设有两个距离对角线同为最远的点 $(x_1,y_1),(x_2,y_2)$，那过这两点的直线与对角线平行，有：

$$ \dfrac{y_2-y_1}{x_2-x_1}=\dfrac{m}{n} $$

但是 $0< x_1<x_2< n,0< y_1<y_2< m$，而 $\gcd(n,m)=1$，所以不存在。

因此，我们说明了在 $\gcd(n,m)=1$ 时，$\mathcal{F}(n,m)$ 中每一个格路的等价类中恰好有 $1$ 条 $(n,m)-\text{Dyck}$ 路。而每一个 $\text{period}$ 都恰好是 $n+m$，因此：

$$ D(n,m)=\dfrac{1}{n+m}F(n,m)=\dfrac{1}{n+m}\binom{n+m}{n} $$

有 $k$ 个峰的 $(n,m)-\text{Dyck}$ 路

对于一条从 $(0, 0)$ 到 $(n, m)$ 的自由路中的连续两步，若其为 $UL$，则我们称之为一个峰；若其为 $LU$，则我们称之为一个谷。

就是凸出来的叫峰，凹下去的叫谷。设 $\mathcal{F}(n,m;k)$ 是有 $k$ 个峰的自由路的集合，$F(n,m;k)$ 是有 $k$ 个峰的自由路的条数。那么有：

$$ F(n,m;k)=\binom{n}{k}\binom{m}{k} $$

设 $k$ 个峰分别是 $(x_1,y_1),(x_2,y_2)\cdots (x_k,y_k)$，有：

$$ 0\le x_1<x_2<\cdots< x_k\le n,0\le y_1<y_2<\cdots< y_k\le m $$

显然选出他们的方案数就是 $\binom{n}{k}\binom{m}{k}$ 的方案数。中间就拿 $LLL\cdots UU$ 接起来就一一对应了。

设 $\mathcal{F}^{UL}(n,m;k)$ 是有 $k$ 个峰，第一步为 $U$，最后一步为 $L$ 的 $(n,m)$ 自由路集合，$F^{UL}(n,m;k)$ 是条数，则有：

$$ F^{UL}(n,m;k)=\binom{n-1}{k-1}\binom{m-1}{k-1} $$

因为第一步是 $U$，所以第一个峰的横坐标已经确定；最后一步是 $L$，所以最后一个峰的纵坐标已经确定。

设 $\mathcal{D}(n,m;k)$ 是有 $k$ 个峰的 $(n,m)-\text{Dyck}$ 路的集合，$D(n,m;k)$ 是有 $k$ 个峰的 $(n,m)-\text{Dyck}$ 路的条数。先给出结论：

$$ D(n,m;k)=\dfrac{1}{k}F^{UL}(n,m;k)=\dfrac{1}{k}\binom{n-1}{k-1}\binom{m-1}{k-1} $$

这指引我们建立 $\mathcal{F}^{UL}(n,m;k)$ 与 $\mathcal{D}(n,m;k)$ 中每个峰的双射。

对于 $P\in \mathcal{F}^{UL}(n,m;k)$，由于第一步是 $U$，最后一步是 $L$，所以恰好有 $k$ 个峰和 $k-1$ 个谷。把路径从谷点划分，变成 $P_1,P_2,\cdots,P_k$ 共 $k$ 部分，其中每一部分都恰好有一个峰。

这 $k$ 个峰可以轮换，每轮换一次就会变成一个 $\mathcal{F}^{UL}(n,m;k)$ 元素。这就说明了 $k$ 个峰可以唯一对应 $\mathcal{F}^{UL}(n,m;k)$ 中的元素。

又对于 $P\in \mathcal{F}^{UL}(n,m;k)$，我们还是想从谷点将 $P$ 拆开。选取在对角线下方最远的格点 $s$，拆成 $P_1,P_2$，根据上文推出过的结论，我们知道这样的点是唯一的，且这恰好可以对应一条 $\mathcal{Dyck}$ 路的一个峰。

所以就证明了：

$$ D(n,m;k)=\dfrac{1}{k}F^{UL}(n,m;k)=\dfrac{1}{k}\binom{n-1}{k-1}\binom{m-1}{k-1} $$

$t-\text{Dyck}$ 路

对于一条从 $(0, 0)$ 到 $(n, m)$ 的自由路，若其始终不经过对角线 $y = t \times x$ 下方，则我们称之为 $t-\text{Dyck}$ 路。特别地，若 $m = t \times n$，则我们称之为 $n$ 阶 $t-\text{Dyck}$ 路。

当 $t=1$ 的时候，答案是为人熟知的卡特兰数。由于 $\gcd(n,t n)=n\ne 1$，所以不能直接用上面的结论。不过注意到 $\gcd(n,t n+1)=1$，套公式得到：

$$ D(n,t n+1;k)=\dfrac{1}{k}\binom{n-1}{k-1}\binom{t\times n}{k-1} $$

现在我们证明 $D(n,tn;k)=D(n,tn+1;k)$。实际上也就是构造一一对应关系：

由于 $\dfrac{tn+1}{n}>t\ge 2$，所以 $\forall P\in\mathcal{D}(n,tn+1;k)$ 的前两步一定都是 $U$。把第一步 $U$ 删去得到 $P'$，现在说明 $P'\in \mathcal{D}(n,tn;k)$。

可以说明，$y=\dfrac{tn+1}{n} x$ 与 $y=tx$ 之间在 $[0,n]$ 上不存在整点，这可以说明 $P'$ 不会一次就掉到 $y=tx$ 下方，因此 $\mathcal{D}(n,tn;k)$ 与 $\mathcal{D}(n,tn+1;k)$ 中的元素一一对应，于是：

$$ D(n,tn;k)=\dfrac{1}{k}\binom{n-1}{k-1}\binom{tn}{k-1} $$

接下来给出 $n$ 阶 $\text{Dyck}$ 路的条数：

$$ D(n,tn)=\dfrac{1}{tn+1}\binom{n+tn}{n} $$

这个可以通过枚举峰的个数来得到：

$$ D(n,tn)=\sum_{k=1}^n D(n,tn;k)=\sum_{k=1}^n \dfrac{1}{k}\binom{n-1}{k-1}\binom{tn}{k-1} $$

注意到 $\binom{n-1}{k-1}$ 可能能帮助我们构造范德蒙德卷积，所以把 $\dfrac{1}{k}$ 分配给 $\binom{tn}{k-1}$，利用等式：

$$ \binom{n}{k}=\dfrac{n}{k}\binom{n-1}{k-1} $$

得到：

$$ D(n,tn)=\sum_{k=1}^n \dfrac{1}{tn+1}\binom{n-1}{k-1}\binom{tn+1}{k} $$

$$ =\dfrac{1}{tn+1}\sum_{k=0}^{n-1}\binom{n-1}{(n-1)-k}\binom{tn+1}{k+1} $$

$$ =\dfrac{1}{tn+1}\binom{tn+n}{n} $$

注意到 $t=1$ 的时候，得到的就是 $\dfrac{1}{n+1}\binom{2n}{n}$，即卡特兰数。推导卡特兰数通项公式的船新角度

接下来给出了一些看起来很厉害的式子，但是我不会证明，而且听说有点问题，所以就不贴上来了。

$\text{Dyck}$ 另一种等价表示

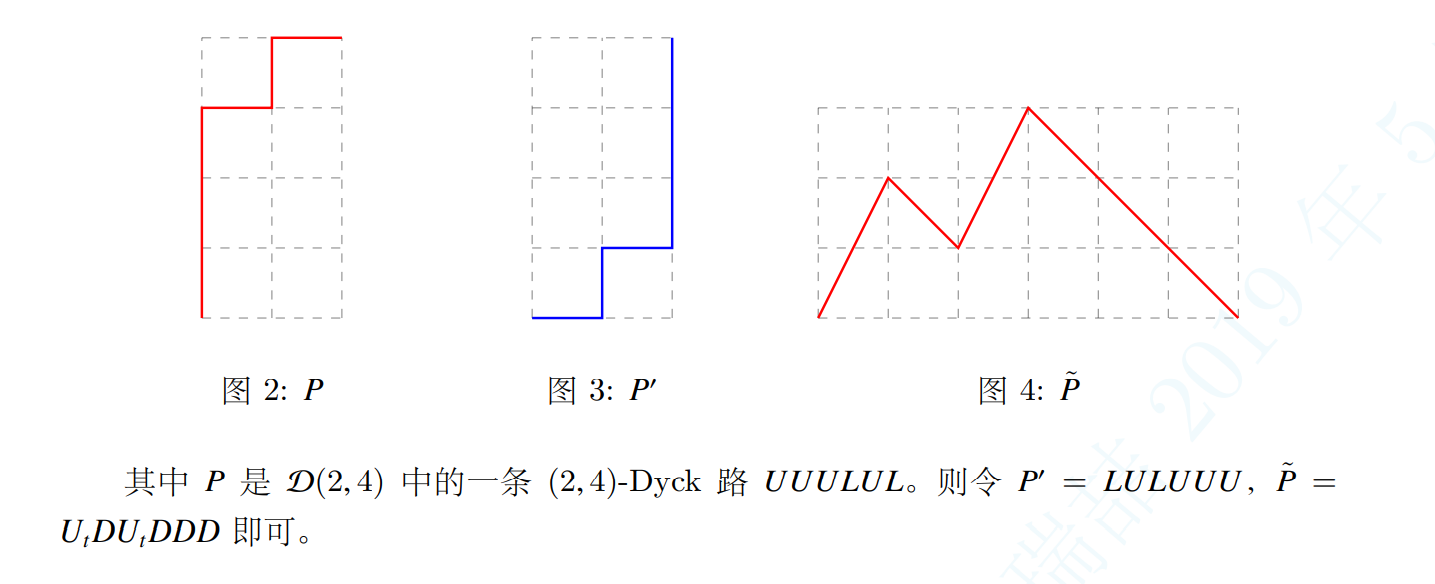
可以把 $U_1$ 定义为 $(+1,+1)$，就是往右上角走；$D$ 定义为 $(+1,-1)$，即往右下角走。则 $n$ 阶 $\text{Dyck}$ 路就是在 $x$ 轴上方，从 $(0,0)$ 走到 $(2n,0)$ 的格路。（这个实际上只要旋转 $45^{\circ}$ 即可得出）

$n$ 阶 $t-\text{Dyck}$ 路等价于把 $U_t$ 定义为 $(+1,+t)$，$D=(+1,-1)$，从 $(0,0)$ 到 $((t+1)n,0)$ 的格路。

可以把 $P\in \mathcal{D}(n,tn)$ $\text{reverse}$，然后把 $L$ 换成 $U_t$，$U$ 换成 $D$，就得到了双射：

不相交格路

$n$ 阶不交 $\text{Dyck}$ 路计数

从 $(0, 0)$ 到 $(n, n)$ 的两条 $\text{Dyck}$ 路 $P,Q$ 称为一个 $n$ 阶 $\text{Dyck}$ 路对。若 $Q$ 始终不穿过 $P$，则 $(P, Q)$ 是一个不交 $\text{Dyck}$ 路对，否则称为相交 $\text{Dyck}$ 路对。

注意这里所说的是穿过，也就是说仅仅有交点是不算相交的。

这东西很像 $\text{LGV}$ 引理干的事情，但是上面的“穿过”的定义有些区别。不过，只要把 $P$ 向左上角移动一格，然后把 $P$ 的首尾都向下延申，变成这样：

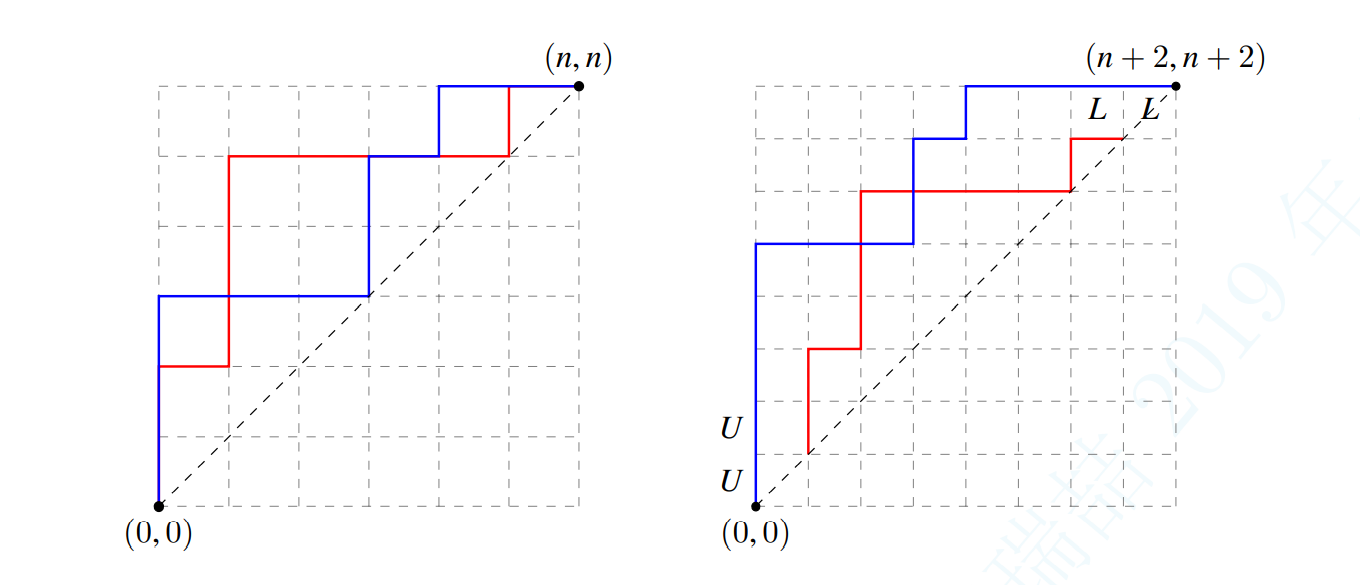
相交的定义就和 $\text{LGV}$ 引理所说的一致了。并且由于要 $P,Q$ 无交点，所以 $P$ 在延申后第一步一定是 $U$，最后一步一定是 $L$，答案不变。而这两条都是 $\text{Dyck}$ 路，所以直接可以卡特兰数。因此可以直接套结论：

$n$ 阶不交 $\text{Dyck}$ 路对数为：

$$ \begin{vmatrix} C_{n} & C_{n+1}\\ C_{n+1} & C_{n+2}\end{vmatrix} $$

其中 $C_n$ 是卡特兰数第 $n$ 项。

还可以拓展到 $k$ 条的情形，估计也是拿 $\text{LGV}$ 引理推的，但是我鸽了。

不交自由路对计数

设 $P, Q$ 是两条自由路，如果 $Q$ 始终不穿越 $P$，则称 $(P, Q)$ 是从 $(0, 0)$ 到 $(n, m)$ 的两条不交自由路对，用 $F_{nc}$ 表示$(\text{non-crossing})$。如果 $P,Q$ 除了起点以及终点之外没有公共点，则称 $(P, Q)$ 是一个不接触自由路对，用 $F_{nt}$ 表示$(\text{non-touching})$。

先来看不接触自由路对，若 $P$ 在 $Q$ 的上方，显然 $P$ 的第一步是 $U$，最后一步是 $L$；$Q$ 的第一步是 $L$，最后一步是 $U$。那把他们缩进去一格，变成了 $(1,0)$ 到 $(n,m-1)$ 和 $(0,1)$ 到 $(n-1,m)$ 的完全不接触的两条路径，直接套 $\text{LGV}$ 可得：

$$ F_{nt}(n,m)=\binom{n+m-2}{n-1}^2-\binom{n+m-2}{n}\binom{n+m-2}{n-2} $$

$$ =\dfrac{1}{n}\binom{n+m-1}{n-1}\binom{n+m-2}{n-1} $$

看起来这个恒等式是平凡的 但是我不会推/hanx

再看不交自由路对，其实把一组不交自由路对 $P,Q$ 中 $P$ 往左上移一格，就变成了一组不接触自由路对，所以：

$$ F_{nc}(n,m)=\dfrac{1}{n+1}\binom{n+m+1}{n}\binom{n+m}{n} $$